지수함수와 로그함수는 서로 역함수 관계에 있습니다.

왼쪽 지수함수는 a(밑)을 y번 곱한 결과값 x 가 중요하고
오른쪽 로그함수(=대수)는 결과값 x 를 알고 있는 상태에서 a 를 몇번 곱해야 하는가의 y 가 중요한 것 이다.
화석의 연대측정에는 방사성 동위 원소 칼륨-40(K-40) 을 사용한다.
칼륨-40(K-40)은 불안정하기 때문에 방사선을 방출하면서 안정상태의 아르곤40으로 변화한다.
이때 방사성원소가 붕괴하여 수가 절반이 되는 기간을 반감기라고 하고 칼륨-40의 반감기는 12.8억년 이다.
우리가 남은 양에 관심이 있다면 아래와 같이 남은 양(=y) 계산을 나타내는 지수함수를 쓸 수 있다.
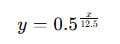
처음으로 부터 12.5억년 지났다면 x = 12.5 이므로 y = 0.5 즉 50% 감소가 되었을 것이다.
하지만 연대 측정에 있어서는 분석을 통해 남은 양을 알고 있으므로 우리가 구하고자 하는 것은 화석이 몇억년 전에 생성된 것 인가이다..
그러므로 우라가 알고자 하는 년대 x 를 왼쪽으로 내세우는 로그함수를 나타낼 수 있다.

위의 상태로는 계산이 어렵기 때문에 (밑의 변환공식) 을 이용한다.

k=10 으로한 상용로그로 변환해 보자.

예를 들어 어느 화석를 조사해 보니 칼륨-40의 양이 40% 라고 하면
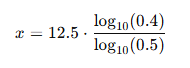
다음은 미리 계산해 둔 상용대수표를 이용하여 값을 구하면 된다.
상용대수표에서는 소수점의 값은 없기 때문에 소수점을 다르게 표현해야 한다.
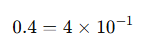

0.5 의 경우도


x = 12.5 x (0.6021 - 1) / (0.6990 - 1) = 12.5 x 1.32 = 16.5 억년
'재미있는 수학' 카테고리의 다른 글
| 인공지능과 미분(체인 룰) (6) | 2025.09.01 |
|---|---|
| 오일러 수 𝑒와 복리, 그리고 인구 증가 이야기 (4) | 2025.09.01 |
| 마이너스 곱하기 마이너스는 왜 플러스 인가요? (2) | 2025.08.30 |