수학에는 오일러 수 e 라는 아주 특별한 숫자가 있습니다.
값은 약 2.718… 인데, 이 숫자는 계속해서 자라나는 것 을 표현할 때 꼭 등장합니다.
1. 복리란 무엇일까?
은행에서 돈을 맡기면 이자가 붙습니다.
- 단리: 원금에만 이자가 붙음 → 매년 같은 금액이 늘어남.
- 복리: 원금 + 이자 전체에 또 이자가 붙음 → 시간이 지날수록 점점 더 빨리 불어남.
예를 들어, 100% 이율로 원금 1을 넣으면:
- 1년에 한 번 복리 → 2가 됨
- 반년에 한 번 복리 → 2.25
- 1년에 4번 복리 → 2.44
- 매달 복리 → 2.61
“계산을 자꾸 더 잘게 나누면 돈이 더 불어나네?”
그런데 아무리 잘게 나눠도 2.718…보다 커지지 않습니다.
이 한계 값이 바로 오일러 수 e 입니다.
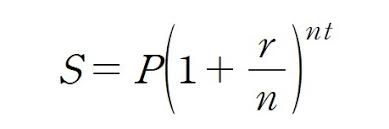
S : t 년후의 원리합계, P : 원금, r : 이자율 , n : 연중 이자 적용 횟수
2. 자연 속의 연속적인 성장
돈뿐만 아니라, 인구, 세균, 바이러스, 방사성 물질 같은 것들도 끊임없이 변합니다.
이때도 오일러 수 e가 등장합니다.
예를 들어, 인구가 계속 5%씩 늘어난다고 하면,
시간 t가 지날수록 인구는 이렇게 불어납니다:

즉, 시간이 지날수록 곡선 모양으로 점점 더 빠르게 늘어납니다.
3. 자연로그란 무엇일까?
반대로, “인구가 몇 배가 되려면 몇 년이 걸릴까?”를 알고 싶을 때는 자연로그를 씁니다.
- 예: 인구가 3배가 되는 데 걸리는 시간은

여기서 ln 이 바로 자연로그예요.
쉽게 말해, ”e를 몇 번 곱해야 원하는 숫자가 되는가?” 를 알려주는 함수입니다.
4. 그림으로 보는 성장
아래 그래프는 초기 인구 1000명, 연 5% 성장을 가정했을 때 50년 동안 어떻게 변하는지를 보여줍니다.
- 직선처럼 보이는 단리보다
- 가속도가 붙는 복리가 더 빠르고,
- 연속 성장(오일러 수 e기반)은 가장 자연스럽고 빠르게 늘어납니다.

5. 정리
- 복리를 무한히 쪼개면 도달하는 값이 바로 오일러 수 e
- 인구 증가, 세균 번식, 질병 확산 등 자연의 성장 법칙은 모두 e를 따른다
- 자연로그 ln 는 이런 성장을 거꾸로 계산할 때 쓰인다
👉 결국, 오일러 수 e는 “자연의 성장 공식”이라고 할 수 있습니다.
'재미있는 수학' 카테고리의 다른 글
| 지수와 로그함수를 알면 화석의 연대 측정이 쉬워진다. (0) | 2025.09.06 |
|---|---|
| 인공지능과 미분(체인 룰) (6) | 2025.09.01 |
| 마이너스 곱하기 마이너스는 왜 플러스 인가요? (2) | 2025.08.30 |