ROC ( Receiver Operating Characteristic) AUC( Area Under the Curve) score 는 binary classifiers의 퍼포먼스 측정에 유명한 메트릭스이다. 평가를 위해선 ROC curve의 밑쪽 면적을 측정하면 다양한 결정 쓰레시홀드에서의 classifier의 평가를 보여준다.
 |
 |
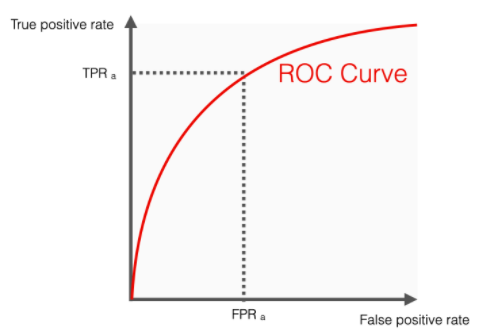
ROC curve는 Y축엔 True Positive rate(TPR=Recall), X축엔 False Positive rate(FPR) 를 플롯
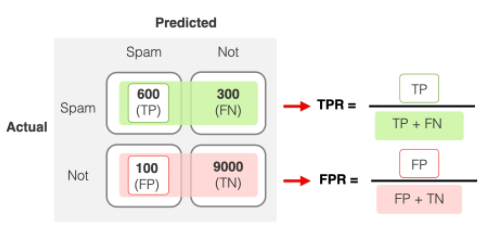
- TPR : 스팸메일에 대해 스팸이라 판단하는 비율
- FPR : 정상메일에 대해 스팸이라 판단하는 비율
binary classifier는 0.5 를 기준으로 판단을 한다. 만약 이 기준(결정 쓰레시홀드)을 임으로 0.1, 0.3, 0.5, 0.7, ... 으로 할 경우, 기준값이 낮아질 수록 False Positive와 True Positive가 동시에 높아지므로 TPR, FPR 동시에 증가하게 되고
기준값이 높아질 수록 반대의 경향이 된다.
이때 곡선이 TPR 쪽으로 굽어 질수록 False Positive는 낮은 것에 비하여 True Positive 는 높게 나타나므로 좋은 모델이라 볼 수 있다. 따라서 곡선밑의 면적이 넓어지게 된다.
추천(=1)일 경우의 확율을 끄집어내서 0에서 1.1로 0.05씩 증가하는 결정 쓰레시홀드를 배열로 만들어 각각의 결과를 통계
|
pos_prob = prediction_prob[:, 1]
thresholds = np.arange(0.0, 1.1, 0.05)
true_pos, false_pos = [0]*len(thresholds), [0]*len(thresholds)
for pred, y in zip(pos_prob, Y_test):
for i, threshold in enumerate(thresholds):
if pred >= threshold:
if y == 1:
true_pos[i] += 1
else:
false_pos[i] += 1
else:
break
n_pos_test = (Y_test == 1).sum()
n_neg_test = (Y_test == 0).sum()
true_pos_rate = [tp / n_pos_test for tp in true_pos]
false_pos_rate = [fp / n_neg_test for fp in false_pos]
|
|
import matplotlib.pyplot as plt
plt.figure()
lw = 2
plt.plot(false_pos_rate, true_pos_rate, color='darkorange', lw=lw)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()
|
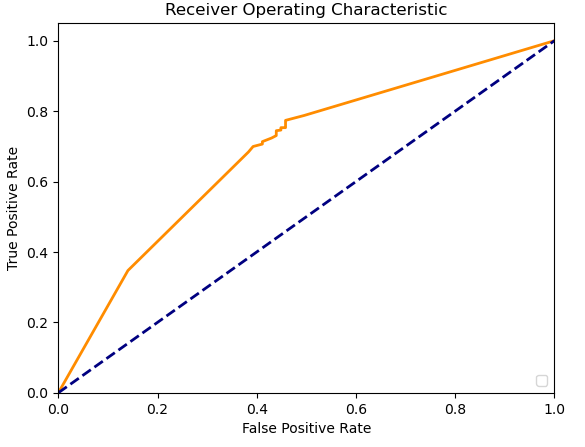
|
from sklearn.metrics import roc_auc_score
print(roc_auc_score(Y_test, pos_prob))
-> 0.6857375752586637
|
'data science > Artificial Intelligence' 카테고리의 다른 글
| SVM(Support Vector Machines) Classifier (0) | 2025.04.02 |
|---|---|
| K-Neighbors Classifier (0) | 2025.04.02 |
| Naïve Bayes (나이브 배이스) Classifier - 실전 2 (0) | 2025.03.08 |
| Naïve Bayes (나이브 배이스) Classifier - 실전 1 (0) | 2025.02.14 |
| Naïve Bayes (나이브 배이스) Classifier (0) | 2025.02.09 |