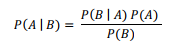 |
B가 true일때 A가 발생할 수 있는 확률은 A가 true일때 B가 발생할 수 있는 확율 곱하기 A의 확률을 B의 확률로 나눈것 (뭔말인지 모르겠다.) |
머신러닝에서 표현하면 아래와 같다.
| B =여러가지 Evidence(=특징) A = Outcome(=결과) P(A | B) = 여러가지 Evidence가 있을 때 Outcome이 나올수 있는 확률(=Likelihood)  |
설명 샘플)
과일(=Outcome)로써 Banana, Orange, Other Fruit 이 있고 특징(=Evidence)으로써 Long, Sweet, Yellow 가 있다고 하자.

| 기본확률 | 값 | Evidence확률 | 값 | ||
| P(Banana) | 0.5 (500/1000) | P(Long) | 0.5 (500/1000) | ||
| P(Orange) | 0.3 (300/1000) | P(Sweet) | 0.65 (650/1000) | ||
| P(Other Fruit) | 0.2 (200/1000) | P(Yellow) | 0.8 (800/1000) |
| P(Evidence | Outcome) | ||
| Banana일때 Long의 확률 | P(Long | Banana) | 0.8 (400/500) |
| Banana일때 Not Long의 확률 | P(Not Long | Banana) | 0.2 (100/500) |
| Orange 일때 Long의 확률 | P(Long | Orange) | 0 (0/300) |
| ... | ||
| Other Fruit 일때 Yellow의 확률 | P(Yellow | Other Fruit) | 0.25 (50/200) |
| Other Fruit 일때 Not Yellow의 확률 | P(Not Yellow | Other Fruit) | 0.75 (150/200) |
만약 어느 과일의 특성이 Long, Sweet, Yellow 의 특성이 강하다고 했을시 어느 과일에 해당되는 확률이 높은지 살펴보자

P(Banana | Long, Sweet, Yellow) = 0.8 * 0.7 * 0.9 * 0.5 / (동일값이므로 무시) = 0.252
P(Orange| Long, Sweet, Yellow) = 0.0 * xx * xx * 0.3 / (동일값이므로 무시) = 0.0
P(Other Fruit| Long, Sweet, Yellow) = 0.5 * 0.75 * 0.25 * 0.2 / (동일값이므로 무시) = 0.01875
결과 Long, Sweet, Yellow 의 특징이 강하다면 Banana 일 확률이 크다.
'data science > Artificial Intelligence' 카테고리의 다른 글
| Naïve Bayes (나이브 배이스) Classifier - 실전 2 (0) | 2025.03.08 |
|---|---|
| Naïve Bayes (나이브 배이스) Classifier - 실전 1 (0) | 2025.02.14 |
| 바이너리 분류 모델에 있어서 평가 항목 (0) | 2024.01.16 |
| 일반 데이터 학습용/테스트용 분리 (0) | 2024.01.14 |
| 학습 데이터 준비 (0) | 2024.01.02 |