digital filters in Python

 

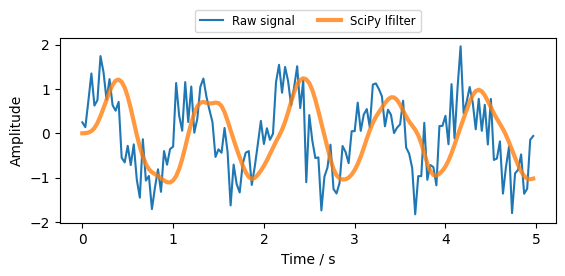
1초간 30 샘플링(30Hz)의 노이즈를 가미한 5초간 진폭이 1Hz 인 사인파를 생성한 후

iirfilter 함수로 N-order = 4,  고주파수 노이즈(>2.5Hz)를 Butterworth 형태의 lowpass 필터의 계수를 구하여 적용한다.

import numpy as np import scipy.signal np.random.seed(42)  # for reproducibility fs = 30  # sampling rate, Hz ts = np.arange(0, 5, 1.0 / fs)  # time vector - 5 seconds ys = np.sin(2*np.pi * 1.0 * ts)  # signal @ 1.0 Hz, without noise yerr = 0.5 * np.random.normal(size=len(ts))  # Gaussian noise yraw = ys + yerr b, a = scipy.signal.iirfilter(4, Wn=2.5, fs=fs, btype="lowpass", ftype="butter") y_lfilter = scipy.signal.lfilter(b, a, yraw) plt.figure(figsize=[6.4, 2.4]) plt.plot(ts, yraw, label="Raw signal") plt.plot(ts, y_lfilter, alpha=0.8, lw=3, label="SciPy lfilter") plt.xlabel("Time / s") plt.ylabel("Amplitude") plt.legend(loc="lower center", bbox_to_anchor=[0.5, 1], ncol=2, fontsize="smaller")

 

IIR Filter (Infinite Impulse Response) : 계속 연결된 신호 (주로 아날로그 신호) 필터

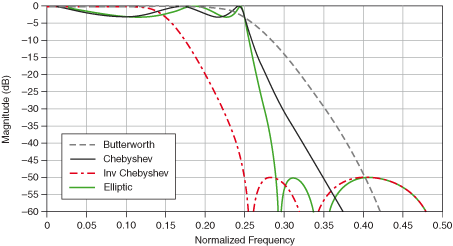
Filter Design 이란 좋은 결과를 얻기 위해 N-order(아래식에서 a, b 계수를 몇개 선택할 것인지) 를 선택하는 것이다.

위에 식에서 보는바와 같이 N 이 클수록 과거 데이터를 많이 사용하므로 계산량도 많아지고 필터가 적용된 그래프와 원래 그래프와의 괘리(Phase shift)가 크개 일어난다.