회전시(반시계 방향)의 변환 매트릭스는 아래와 같다.

이 매트릭스가 되는 이유는 아래와 같이 삼각함수로 설명이 가능하다.
x좌표(1, 0)를 θ만큼 회전을 시키면 삼각함수 cosθ = x' / 1 과 sinθ = x' / 1 에 의해 x' = cosθ, sinθ 가 된다.
y좌표(0, 1)를 θ만큼 회전을 시키면 삼각함수 sinθ = y' / 1(음수값이므로 -) 과 cosθ = y' / 1 에 의해 y' = -sinθ, cosθ 가 된다.
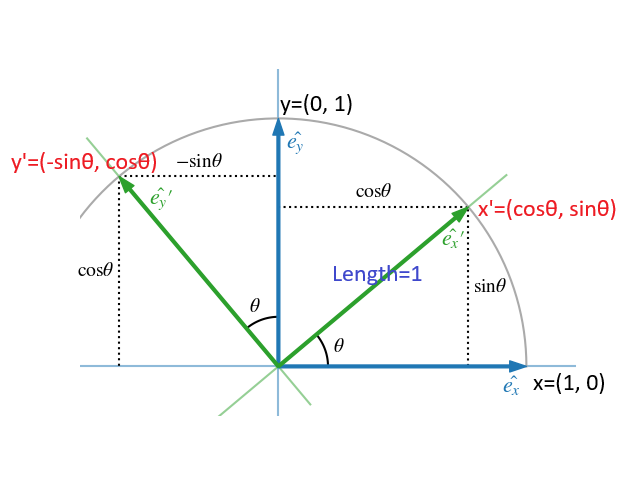
여기에 회전후 좌표 이동까지 고려한다면 아래와 같다.

이에 상응하는 OpenCV 함수는 아래와 같고

리턴하는 매트릭스는 위의 2 x 3 의 형태가 된다.

위의 매트릭스를 이미지에 적용하는 함수는 warpAffine() 이다.
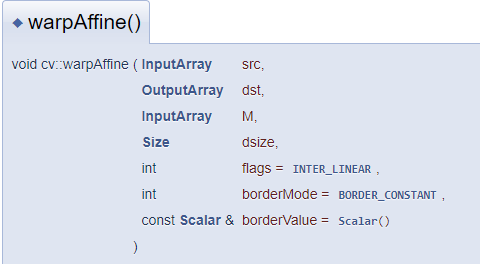
1. 일반 회전
| cv::Mat image = cv::imread("d:\\rotate.png"); cv::Point2f centre(image.cols / 2., image.rows / 2.); cv::Mat M = cv::getRotationMatrix2D(centre, 23, 1.0); cv::Mat image2; cv::warpAffine(image, image2, M, image.size(), cv::INTER_AREA); cv::imwrite("d:\\rotate1.jpg", image2); |
결과는 반시계 방향으로 23도 회전 되었다.
 |
 |
문제는 최종 사이즈 image.size() 에 의해 컷팅당하는 것이다.
2. 회전 & 전체 표시
| cv::Mat image = cv::imread("d:\\rotate.png"); cv::Point2f centre(image.cols / 2., image.rows / 2.); cv::Mat M = getRotationMatrix2D(centre, 23, 1.0); cv::Rect2f bbox = cv::RotatedRect(cv::Point2f(), image.size(), static_cast<float>(23)).boundingRect2f(); M.at<double>(0, 2) = M.at<double>(0, 2) + bbox.width / 2.0 - image.cols / 2.0; M.at<double>(1, 2) = M.at<double>(1, 2) + bbox.height / 2.0 - image.rows / 2.0; cv::Mat image2; cv::warpAffine(image, image2, M, bbox, cv::INTER_AREA); cv::imwrite("d:\\rotate1.jpg", image2); |
포인트는 cv::RotatedRect() 함수를 이용하여 회전후의 풀사이즈를 얻어서
매트릭스(M)의 이동계수(매트릭스 각 로우의 맨 마지막)를 풀사이즈와 컷팅사이즈 차분의 절반(센터 좌우 고려) 만큼 더 이동시켜 주면 OK

'opencv' 카테고리의 다른 글
| b/w 이미지의 칼럼(수직방향)별 검정(=0)픽셀수 카운트 (0) | 2023.12.02 |
|---|---|
| cv::Mat 이모저모 (1) | 2023.11.29 |
| 스캔문서의 기울기 알아보기 - 2 (0) | 2023.11.27 |
| 스캔문서의 기울기 알아보기 (0) | 2023.11.26 |
| (opencv) 이미지 저장형태, 액서스 (1) | 2023.11.25 |