인공지능과 미분(체인 룰)
1. 신경망 구조 살펴보기
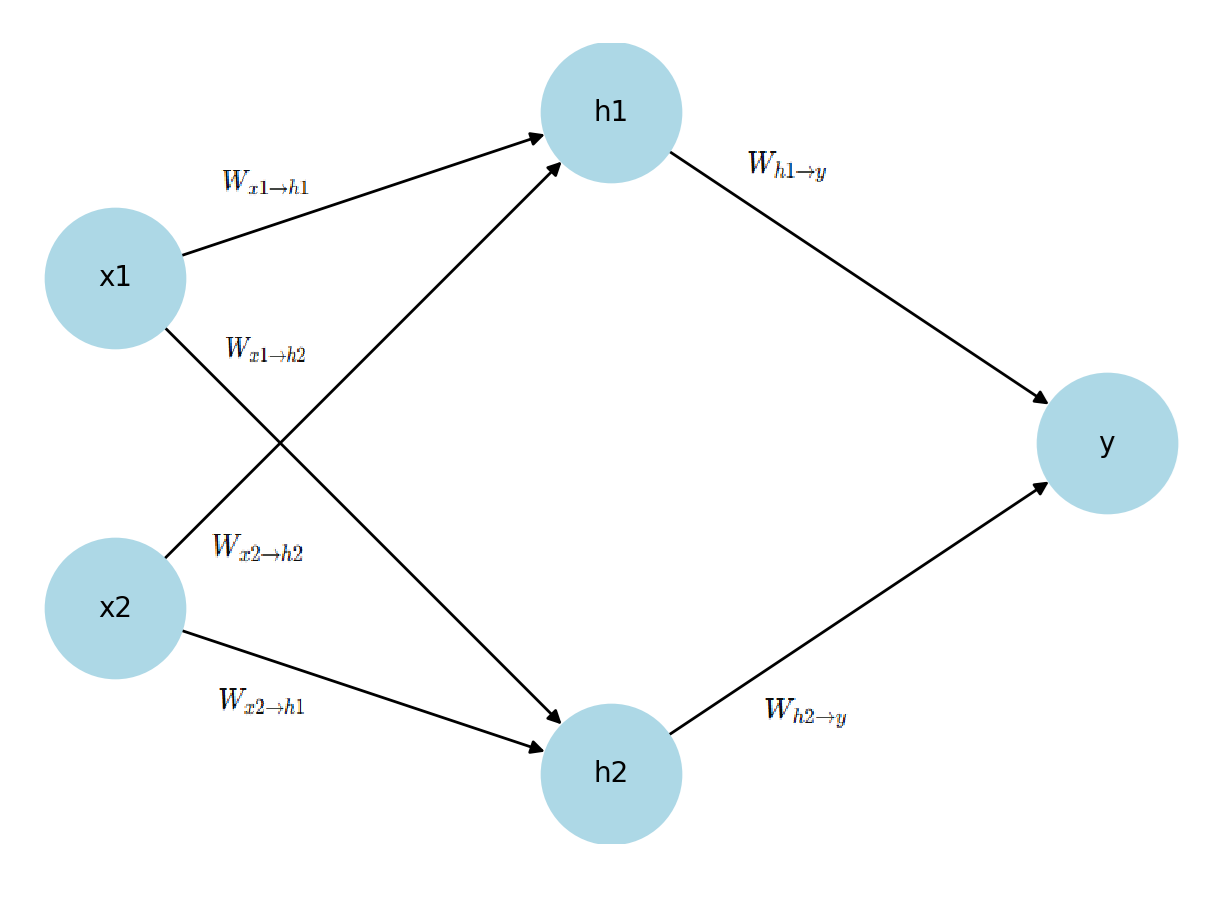
아래 그림은 아주 단순한 신경망 구조입니다. (bias는 설명을 간소화하기 위해 생략)
- 입력층(Input Layer): x1,x2x_1, x_2
- 은닉층(Hidden Layer): h1,h2h_1, h_2
- 출력층(Output Layer): yy
신경망 학습의 목적은 로스(Loss, 오차) 를 줄이도록 가중치(Weight) 를 조정하는 것입니다.
 |
|
2. 로스(Loss)란 무엇인가?
예측값은 정답과 차이가 있습니다. 이 차이를 수치로 나타낸 것이 로스 함수(loss function) 입니다.
예시:
- 정답: 고양이(1)
- 예측: 0.7
- 로스: (1−0.7)2=0.09(1 - 0.7)^2 = 0.09
👉 즉, 로스는 얼마나 틀렸는지를 알려주는 지표입니다.
신경망 학습은 Forward → Loss 계산 → Backpropagation(역전파) 의 반복으로 진행됩니다.
3. Backpropagation(역전파)의 개념
목표는 오차(Loss)를 최소화하는 것. 오차는 가중치 w 에 따라 변합니다.
아래 그림은 단순화를 위해 가중치 하나 w 와 로스 함수의 관계를 표현한 것입니다.
- 가중치 값 w 에 따라 로스 값이 달라집니다.
- 로스가 최소가 되는 지점은 w=3.
- 현재 학습으로 얻은 w=5 라면, 어떻게 하면 w=3 방향으로 이동할 수 있을까요?

4. 미분(Gradient)의 필요성
이 문제를 해결하기 위해 미분(derivative) 이 필요합니다.
- 미분은 한 지점에서 함수의 변화율(기울기, gradient) 을 나타냅니다.
- 예: w= 에서의 기울기가 양수라면, 오른쪽으로 갈수록 값이 커진다는 의미 → 따라서 로스를 줄이려면 왼쪽(– 방향) 으로 이동해야 합니다.
즉, 미분은 어느 방향으로 가야 로스가 줄어드는지를 알려주는 나침반 역할을 합니다.
5. 가중치 업데이트 공식
가중치는 다음과 같이 업데이트됩니다:

- 방향: - 를 하는 이유는 기울기와 반대편으로 이동해야 하기 때문
- 이동량: 학습률(η, learning rate) × 기울기(gradient)
👉 학습률 η 는 "한 번의 업데이트에서 얼마나 크게 이동할 것인가"를 결정합니다.
- 너무 크면: 최적점을 지나쳐버림
- 너무 작으면: 학습이 너무 느려짐
6. 신경망 전체에 적용 (체인룰)
실제 신경망에서는 로스 함수가 훨씬 복잡합니다.

여러 층(layer)의 w 와 h 가 얽혀 있기 때문에, 체인룰(Chain Rule) 을 이용해서 각 층의 기울기를 순서대로 계산합니다.
이렇게 출력층에서 시작해 입력층까지 기울기를 전파하는 과정을 Backpropagation(역전파) 라고 합니다.
심플한 체인룰


7. 예제: 간단한 신경망
- 입력: x1=1.0, x2=2.0
- 정답: t=1.0
- 파라미터: w11=0.1, w21=0.2, b1=0.0, w2=0.5, b2=0.0
Forward: 출력과 로스를 계산

Backward: 각 파라미터의 gradient 계산 (∂L / ∂w, ∂L / ∂b)

※ y, u, h 의 기울기는 다음 w와 b의 기울기를 계산하기 위해 사용됩니다.
※ b1의 미분은 h 기울기, b2의 미분은 u의 기울기
※ 계산의 간편화를 위해 h 와 활성화 함수는 입력값 = 출력값 (예: y=x) 으로 미분은 1 이 되게 했습니다.
Update:
위의 각각 결과값들을 learning rate(η=0.1) 를 이용해서 업데이트를 한다.

예) w2 = w2 - (0.1) x (-0.375) = 0.5 + 0.0375 = 0.5375